Distributionally Robust Bayesian Optimization
Abstract
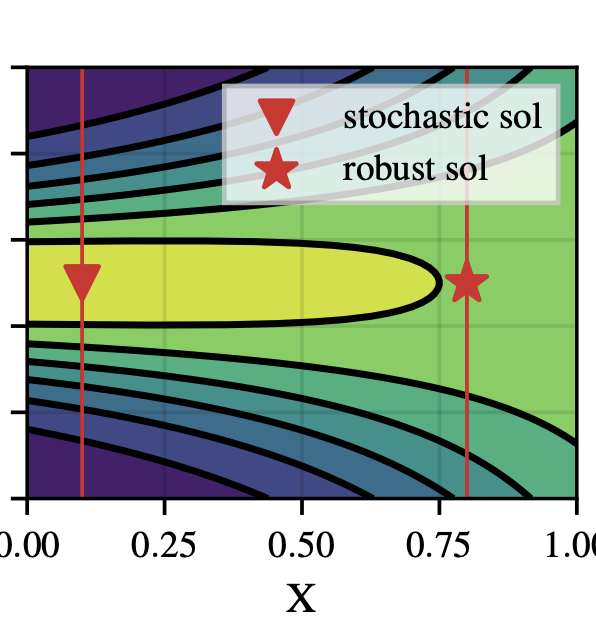
Robustness to distributional shift is one of the key challenges of contemporary machine learning. Attaining such robustness is the goal of distributionally robust optimization, which seeks a solution to an optimization problem that is worst-case robust under a specified distributional shift of an uncontrolled covariate. In this paper, we study such a problem when the distributional shift is measured via the maximum mean discrepancy (MMD). For the setting of zeroth-order, noisy optimization, we present a novel distributionally robust Bayesian optimization algorithm (DRBO). Our algorithm provably obtains sub-linear robust regret in various settings that differ in how the uncertain covariate is observed. We demonstrate the robust performance of our method on both synthetic and real-world benchmarks.