Robust Best-arm Identification in Linear Bandits
Abstract
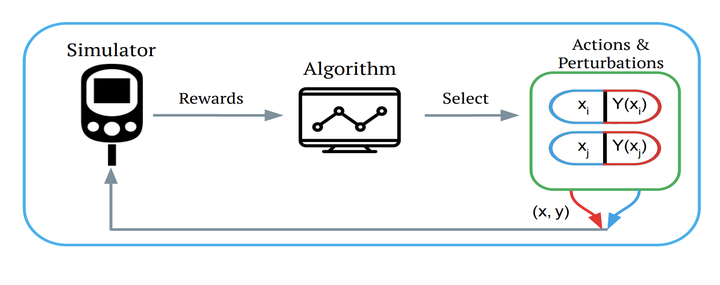
We study the robust best-arm identification problem (RBAI) in the case of linear rewards. The primary objective is to identify a near-optimal robust arm, which involves selecting arms at every round and assessing their robustness by exploring potential adversarial actions. This approach is particularly relevant when utilizing a simulator and seeking to identify a robust solution for real-world transfer. To this end, we present an instance-dependent lower bound for the robust best-arm identification problem with linear rewards. Furthermore, we propose both static and adaptive bandit algorithms that achieve sample complexity that matches the lower bound. In synthetic experiments, our algorithms effectively identify the best robust arm and perform similarly to the oracle strategy. As an application, we examine diabetes care and the process of learning insulin dose recommendations that are robust with respect to inaccuracies in standard calculators. Our algorithms prove to be effective in identifying robust dosage values across various age ranges of patients.