Stochastic Linear Bandits Robust to Adversarial Attacks

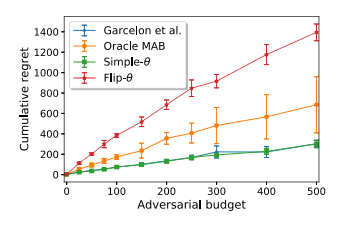
Abstract

We consider a stochastic linear bandit problem in which the rewards are not only subject to random noise, but also adversarial attacks subject to a suitable budget C (i.e., an upper bound on the sum of corruption magnitudes across the time horizon). We provide two variants of a Robust Phased Elimination algorithm, one that knows C and one that does not. Both variants are shown to attain near-optimal regret in the non-corrupted case C=0, while incurring additional additive terms respectively having a linear and quadratic dependency on C in general. We present algorithm independent lower bounds showing that these additive terms are near-optimal. In addition, in a contextual setting, we revisit a setup of diverse contexts, and show that a simple greedy algorithm is provably robust with a near-optimal additive regret term, despite performing no explicit exploration and not knowing C.